Things should be as simple as possible but not simpler.
-Albert Einstein
Note: I use some equations in this post that might appear formatted weird in email as opposed to the website. I recommend viewing it on Substack directly.
Most problems worth solving are high dimensional problems. A high dimensional space is a problem space controlled by many variables. Whether you’re talking about understanding socioeconomic dynamics, the design of a vehicle, determining what your fans are responding to, understanding our genetics, or how to build your business, they all operate in high dimensional spaces. Unfortunately, people don't have intuition for high dimensional spaces. That's why we build mathematical models to tease apart the relationships in these complex environments. Many people think they can intuitively solve problems with many variables but I'm here to tell you that isn't true. I can show you where your intuition fails with the four circle paradox which I originally learned from Richard Hamming in The Art of Doing Science and Engineering.
The Four Circle Paradox
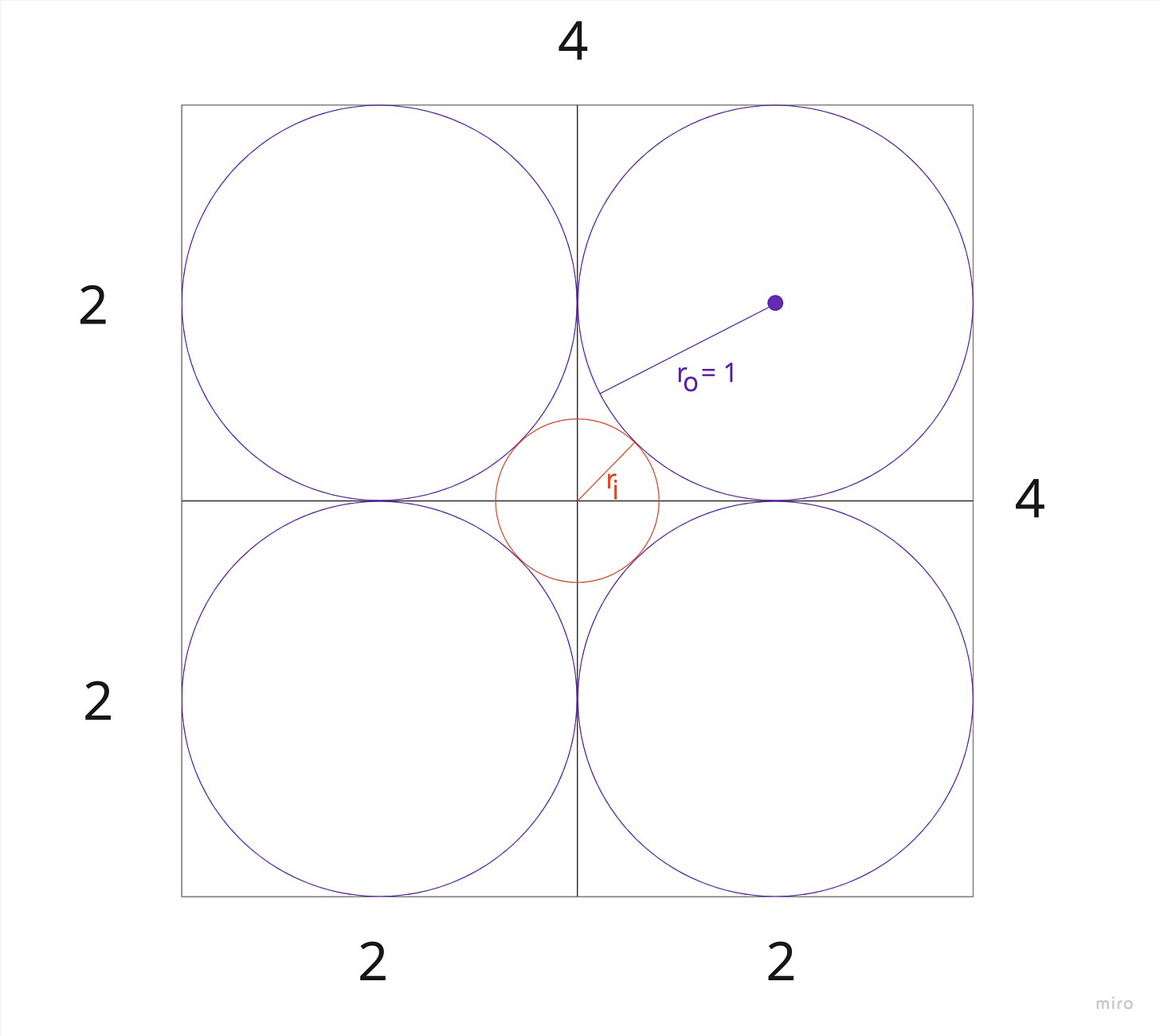
Let's start with the following premise. Say I draw four unit circles and bound each of them in a square. A unit circle has a radius equal to one. Connecting the squares makes a large square measuring four units by four units. Now my goal is to draw an inner circle at the center of the larger square that tangentially touches each of the other circles. See Figure 1 below for a visualization.
What's the radius of the inner circle?
Figure 1. Illustrating the four circle paradox in two dimensions
In two dimensions we can compute the radius of the inner circle as the hypotenuse of a right isosceles triangle with legs of unit length and subtracting the unit radius of the outer sphere.
Simple enough. Now let's start moving up dimensions such that we have 4*(n-1) circle like objects - circle, sphere, n-sphere, etc., controlled by equations such that each point on the edge is the same distance r, the radius, from the center and where n is the number of dimensions. If we move from two to three dimensions, the circles become spheres, the squares become cubes, and an additional layer of spheres and cubes must be added. This totals 8 outer unit spheres inside of 8 cubes. Now we determine the radius of a single inner sphere made tangential to all 8 unit spheres. In three dimensions the radius of inner sphere can be reduced to the following using the euclidean distance:
we can generalize this equation to n dimensions such that
Do you agree? Really think about it.
Why should this give you pause? Well let's look at 10 dimensions, which is more dimensions than the human mind can visualize but is tiny compared to the typical mathematical high dimensional space dealt with in complex models.
Why is that an issue? Why is that a paradox? Well for ten dimensions, the radius of the inner 10-dimensional sphere is larger than 2 which is the width of the box surrounding the outer unit 10-sphere. In order to touch all the other outer ten-dimensional unit spheres, the inner ten-dimensional sphere actually reaches outside the bounds of the boxes we set around the outer spheres! Is that something you even considered or thought of while you worked through this simple problem? Imagine how your intuition might fail you for more complex high dimensional problems. High dimensions are unintuitive!
Now let's take it to 1000 dimensions.
The inner sphere is an order of magnitude larger than the outer unit spheres that it is supposed to be touching. Is your intuition accounting for that?
Implications
Why does this matter? Are you working on a problem that has many variables and is thus a high dimensional space? Your intuition is probably failing you and causing your decision making to be subpar. Perhaps failures are occurring in your solution that you are not expecting. Even some mathematical models can struggle in high dimensional spaces. This is typically called the curse of dimensionality.
It also matters because as you use large language models and AI agents more, you need an understanding of where they might fail you. There's been a lot of talk recently about vector databases and how to optimize them in order to help prompt large language models. Both large language models and vector databases use embeddings which is a way to compress a concept or data structure mathematically. By searching for embeddings that are close to each other you can find similar concepts, think queen and king, or in the case of prompting large language models, the correct recipe for your question about what uses carrots and soy sauce. Try playing this game to get an better understanding of how embeddings work. These embeddings are typically on the order of 500-1000 variables, very high dimensional space. At that scale, objects that are you might consider similar can still be relatively close to objects that are dissimilar, because everything is so far from each other. Think of it as the difference between point A being a distance of 10,000,000,000 miles from a similar point B and 10,000,200,000 miles from a dissimilar point C. Point B is definitely closer to point A than point C but the relative distance between points B and C is very close. Both points are also really far away from point A. The difference could be a rounding or measurement error.
What can you do? It's rough out there and you still need to solve problems. You can't just let a high dimensional space prevent you from doing things.
First it is always good to understand where your decision making has limits and where it can be error prone. Use this understanding to apply your decision frameworks in the right environments.
Find ways to test and measure your decision making to make sure you are on track and have ways to test for issues that can occur in high dimensional spaces.
Use mathematical models to understand and interpret different aspects of your problem. However, remember there may still be issues you will need to address in high dimensional spaces.
Collect more data. It isn't always feasible but when possible, more data can help a lot with some dimensionality problems. However, beware of searching through spurious correlations.
Find ways to reduce the dimensionality of your problem. It might not be fully correct and you might lose information by reducing the number of variable but it has a good chance of improving your performance and your ability to think about a problem.